Вернуться на страницу ежегодника Следующая статья
I. Historical aspects
An Investigation of the Relationships between Empirical Trends in Both Entropy and Maximum Urban Area Size Over the Last 5,000 Years (Download pdf)
DOI: https://doi.org/10.30884/978-5-7057-6233-0_02
Antony Harper, Independent Scholar
Abstract
Keywords: entropy, maximum urban area size, stasis, punctuation, skeletoni-zation.
Introduction
The intent of this paper is to relate entropy to the set of world-system population, maximum urban area, and γ, a fitted constant, data on a century-by-century basis over the last 5,000 years of human history. This will be done using the Shannon entropy equation (Shannon 1948).
The previous paper, which involved the analysis of a three differential equation model of punctuated equilibrium patterns, used entropy as a unifying concept between the three salient variables of that model: population size, carrying capacity, and technology. Previously (Harper 2017a) this model was introduced and shown to produce the behavior of stasis and punctuation as represented by the distribution of maximum urban area population magnitudes over time. For a more detailed description of this model the empirical data for maximum urban area magnitude, Cmax, were natural log-transformed to reveal a stepwise pattern suggestive of punctuated equilibrium as first suggested by Eldredge and Gould (1972) and later incorporated into a more general description of system behavior by the late Per Bak, in his book entitled, How Nature Works: The Science of Self-Organized Criticality (1996) and in a number of research papers, for example Bak and Sneppen (1993). However, with the publication of the paper ‘Integration of Disparate Processes’ there arose a question as to how the variables, N, K, and T are related to one another and what interchangeable units could be used to show these relationships. The analysis of assessing each variable in terms of the others was quite unfruitful. However, on describing this problem to Claudio Maccone[1], he suggested equating each variable as represented by their specific differential equation to a fourth variable, entropy, and doing so using a continuous version of the Shannon Entropy Equation, H = -∫f(x)lnf(x)dx. It should be noted here that this is not the first time that the concept of entropy has been applied to sociological-demographic theory and practice. Bailey (1990) has previously done this, calling his model social entropy (SE) and paralleling its development with that of physical entropy, developed by the pioneers of that concept (e.g., Boltzman and others). Any standard book on physics will give a decent explanation of entropy, e.g. see Tiner (2006). However, that approach and focus is not directly applicable here. Rather, entropy as it applies to the pattern of punctuated equilibria exhibited by the distribution of ln Cmax over historic time will be the focus.
A quick excursion back to the initial paper ‘The Integration of Two Disparate Processes’ is necessary to reveal a paper's intent. Using the software, STELLA, runs of the three-equation punctuated equilibrium model and their entropy equivalents were examined and it was found that entropy minima were temporally coincident either with the initiation of a punctuation phase or were one time step preceding that initiation. The former occurred with population, N, and the latter with technology, T. Carrying capacity, K, exhibited patterns of continuous change but not of punctuation; the continuously changing carrying capacity exhibited further change in either decreasing or increasing slope. This description of the three-equation model and its entropy transformation is necessary as it gives context in which comparisons may be made with entropy changes based on empirical data.
As will be explained below (in the Materials and Methods section) and in further mathematical detail in the Appendix, the calculation of H = -Σpilnpi per century is dependent on an assumption of urban area sizes that follow a predictable distribution. As these sizes fall into a series of growing urban area groups of the same urban area size, the math of sequences and series will be employed to determine prechosen even divisions that can then be used to determine the value of pi as it is used in the calculation of H.
It is the intent of this paper to show that entropy changes over historic time follow an alternating pattern of entropy decrease followed by entropy increase. Further, it will be shown that these alternating entropy states, either decreasing or increasing, are embedded within alternating linear and non-linear phases, the latter being modeled as quadratic. Finally, linear phases alternate between negative and positive slopes, and quadratic phases alternate between positions of concave up and concave down. So, the overall pattern might begin with a quadratic concave up followed by a linear phase with a negative slope, followed by a quadratic phase which is concave down, followed by a linear phase with a positive slope.
Materials and Methods
All graphs and most numerical analyses were done using the on-line software, SciDAVid. This software not only plots in a variety of modes, for example scatter, spline, etc., but also permits a variety of numerical analysis to be done, including but not limited to both linear and non-linear regression and goodness of fit of the regressions, here employing the Coefficient of Determination. All data used were as previously mentioned in other publications, for example Harper (2017a, 2017b, 2019) a combination of maximum urban area population magnitudes fr om Modelski (2003), 3000 BCE to 2000 BCE, and fr om Chandler (1987), fr om 2000 BCE to 2000 CE. The historical estimates of world-system population magnitudes over the last 5,000 years were accessed at the U.S. Census Bureau[2], and all computed values of the variable, γ, were the result of numerical solutions of the equation: Cmaxγ- Cmax- (γ – 1)T = 0 (Harper 2010). A TI-84+ calculator was used for all hand computations. Computing the value of H per century was a complex, multi-step process, and the algorithm of these computations is given in the Appendix.
Results
In this section, instead of tediously describing each graphical data set and in places the equation(s) modeling those patterns, a graphical summary and accompanying text of the different data sets will be given with the significance of the data displayed being treated in the Discussion section.
To begin, von Foerster (1960), and with greater mathematical clarity, Korotayev et al. (2006) demonstrated the phenomenon of hyperbolic (human) population growth, represented elegantly by the equation,
Nt = C/(to – t), (Eq. 1)
where C is a fitted constant, to represents some transition point at which population growth enters what Korotayev et al. have labeled as the ‘blow-up phase’ (see Fig. 1a), and t is simply the variable, time, moving forward. When entropy is calculated based on the same data, T, Cmax, and γ, per century and plotted over the same period of time the same graphical form is produced, that is entropy change over time is hyperbolic (see Fig. 1b). In fact, the entropy graph writ large is at least a fraternal twin of the population graph over the same period and conceivably could be modeled by the same form of equation. It should be no-ted here that the fine(r) structure of these two graphs does differ. This can be seen in Fig. 2.
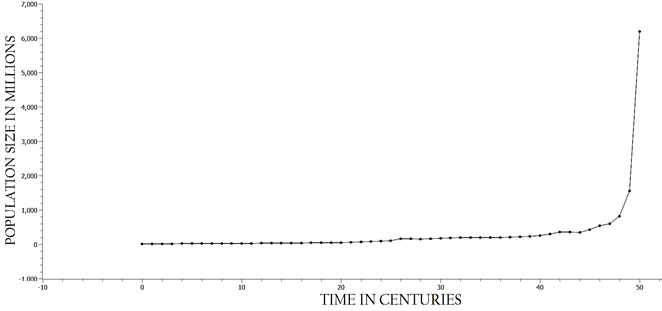
Fig. 1a. World-System Population Over Time. The X-axis represents time in centuries, and the Y-axis represents world-system population magnitude. Note the rapid upturn of this plot, an upturn that is the ‘blow-up phase’
.png)
Fig. 1b. The X-axis represents time, and the Y-axis represents entropy, H, as evaluated in the Appendix. Note the ‘blow-up phase’ of this graph at the far right-hand side
By removing the final point of the entropy curve in Fig. 1b the fine scale of that graph can be seen more clearly (see Fig. 2). This graphical morphology will be compared with a similarly reduced graph of the plot in Fig. 1a. At present, it is quite clear that the finer scale of entropy revealed is anything but the quasi-linear appearance of the first 4,800 years of human history that is represented in both Figs 1a and 1b. This graph consists of a series of oscillations over time with some considerable noise that produces the fluctuations about a fundamental pattern that will become clear shortly. One should note that what is being called noise here has real historical meaning, but not directly with respect to the overall pattern displayed in the graph, that is the associated historical processes and events have to be aligned with the ‘noise’ in question.
.png)
Fig. 2. Entropy change over time. X-axis (fr om 3000 BCE – 1900 CE), and Y-axis as above. By removing the last point, 2000 CE, the fine scale of entropy change over the last 4,900 years of change can be displayed in more detail
If we remove the key outlier points from the graph in Fig. 2, one can clearly see the basic pattern (see Fig. 3), in which the periods of decreasing entropy alternate with the periods of increasing entropy. Specifically, there are four periods of decreasing entropy: Period 1 from 3000 BCE to 1900 BCE; Period 2 from 1200 BCE to 700 BCE; Period 3 from 200 CE to 700 CE; and Period 4 from 1000 CE to 1800 CE. The alternate periods of entropy increase are: Period 1 1900 BCE to 1200 BCE; Period 2 from 700 BCE to 200 CE; Period 3 from 700 CE to 1000 CE; and Period 4 from 1800 CE to 2000 CE. Two points of significance with respect to this pattern need to be mentioned.
.png)
Fig. 3. Skeletonized entropy change over time. The X-axis is time, and the Y-axis is entropy as measured by H
First, the actual entropy peaks and troughs are not necessarily on century marks. For instance, the period between 100 BCE and 200 CE is a case in point in which the actual intersection of increasing and decreasing trends is not coterminal with any century mark. Second, all these entropy designations are approximations and are meant to represent overall trends only. Nevertheless, these trends reveal interesting information both on their own and in comparison, as will be shown in the Discussion section.
Fig. 4 represents a stacked two-level representation of both the non-skeletonized and skeletonized of the entropy trends in Figs 2 and 3. This comparative graphical setting allows the reader to see what specific points have been removed during the skeletonization process, points that none the less have historical significance, for example note the trough between 200 CE and 1000 CE in which the downside, that is the left side of the trough which has a negative slope, represents a period of time in which both the Roman and Han empires declined. It should be mentioned (parenthetically) that increasing entropy periods represent a decrease in order, while the periods of decreasing entropy represent the periods of increasing order.
![]()
![]()
![]()
![]()
.png)
Fig. 4. A comparison of skeletonized and non-skeletonized entropy change over time. A two-panel graph of entropy change over time in which the top graph represents an unskeletonized plot, with the exception of the removal of data for 2000 CE and the bottom panel represents a skeletonized plot
In both the skeletonized and unskeletonized graphs there are four entropy minima and four entropy maxima, all of which correspond to minima and maxima of the graph of lnCmax over the same period of time. There are three of these minima which represent tipping points of the lnCmax plot. These three points are world-system-wide minima characterized by Cmax/T ≤.0014 and are historical tipping points in that they represent the initiation of significant positive trends, for example the approximate beginning of the Industrial Revolution (see Fig. 5).
Fig. 5 represents an extension of the two stacked graph above in which a third layer at the bottom has been added in which further skeletonization has been applied giving three sets of declining entropy trends and three of increasing entropy trends. The upper two layers are as in Fig. 4. In the bottom layer of Fig. 5 the points associated with a single pair of entropy decline and increase from 200 CE to 1000 CE have been eliminated. This skeletonization then gives what appears to be a continuous, curvilinear structure from 700 BCE to 1800 CE. In particular, excluding the paucity of points between 200 CE and 1000 CE, it suggests an overall pattern in which there are three periods of entropy decrease interspersed with three periods of increase.
![]()
![]()
![]()
![]()
.png)
Fig. 5. A comparison of further skeletonization of entropy change over time. The axes are scaled as above. The top two panels are a repeat of what was displayed in Fig. 4, but the bottom graph exhibits the effect of further skeletonization, and as a consequence reduces the system to three periods of entropy decrease interspersed between three periods of entropy increase
An overlay graph of both the totally unskeletonized and skeletonized graphs is given in Fig. 6. In this graph there are numerous portions exhibiting digressions from the overall but, as I believe, fundamental pattern which is due to skeletonization. As already mentioned, the trough between 200 CE and 1000 CE is one instance of this digression, as is the oscillatory pattern from 2400 BCE to 1900 BCE. Both of these instances represent significant changes in entropy beyond the general trends produced by skeletonization of the original data.
![]()
.png)
Fig. 6. An overlay of skeletonized and non-skeletonized entropy data over time. Axes as previously. This graph represents an overlay of the data in the bottom panel of Fig. 5 overlaying the data of a non-skeletonized graph between 3000 BCE and 1800 CE. The intent here is to show which data was removed. Further, this graph should give pause for thought with respect to the historical processes and events that diverged from the skeletonized pattern
One should remember that the curvilinear nature of the trend from 700 BCE to 1800 CE will be returned to for a numerical analysis of its non-linear nature.
Now it is time to turn to a comparison of the entropy graphs with those representing changes in lnCmax over the same 5000-year period. The log-transform, using logarithms to the base e was employed as the range of maximum urban area population size was so large that the larger values, when plotted, literally obliterated the urban area size patterns at earlier and much smaller values. This alteration has been previously done in other papers for the same purpose (see, e.g., Harper 2017a, 2017b). In Fig. 7 a two-layered presentation is given in which the top layer is the skeletonized entropy graph and the bottom layer is the unskeletonized lnCmax graph. There are a number of coterminous points of interest. Minima in both graphs occur at 1900 BCE and 700 BCE, and although appearances can be misleading also at 1800 BCE; lnCmax is graphed in Fig. 7, not Cmax/T, however, these minima all correspond to the minima for Cmax/T ≤.0014. It is evident that each graph in Fig. 7 shares aspects in common with the other, and other than a set of coterminous points. The periods of stasis in the lnCmax graph correspond to the periods of declining entropy, while periods of rapid growth in Cmax, that is the periods of punctuation, correspond to the periods of increased entropy. Specifically, these processes of entropy change and change in Cmax as reflected by the log-transformed data, as has been previously mentioned, have beginnings and endings that are coterminous points and now become beginnings and endings of phases of entropy changes.
![]()
.png)
Fig. 7. A comparison of skeletonized entropy trends over time with log-transformed maximum urban area size
This finding should not be surprising, as the same data, differently treated of course, are used as the basis of each graph. However, identifying the connection between entropy change, either increasing or decreasing, with punctuation and stasis is significant (for more detailed information see the Discussion section). Fig. 8 shows the skeletonized graph of the bottom panel of Fig. 7, so that we can compare these two graphs subject to the same process of simplification, that is skeletonization. It is quite apparent that the similarities between these two graphs discussed above are more clearly displayed and affirm the parallel character of the phases of punctuation and increasing entropy and phases of stasis and decreasing entropy.
![]()
![]()
![]()
![]()
![]()
.png)
Fig. 8. A comparison of the skeletonization of both
entropy and maximum urban area trends over time. The top panel has axes
as previously defined, however, the bottom panel has a ske-letonized version of the natural log-transformed data for Cmax, i.e. the Y-axis represents this log-transformed data. The
X-axis is time
It is important here to return to the skeletonized graph of entropy change over time as represented in the top panel of Fig. 7 to consider the scatterplot from 700 BCE to 1800 CE. The distribution appears to be parabolic and concave down and is more clearly represented in Fig. 9, having a second order poly-nomial regression with a best fit equation applied to this data:
Y = –1.3625 + .1356X – .0019X2, R2 = .9469. (Eq. 2)
It follows that a quadratic is a reasonable choice of curves. One should note that when regressions of higher order polynomials were generated, the coefficient of determination did increase, however, given the already excellent fit of data to a second order regression and always relying on Occam's Razor, I have chosen to remain with the simplest equational fit. More significantly, this model of underlying pattern includes both an entropy increase, from the beginning of the curve at 700 BCE to approximately 500 CE and a phase of entropy decrease from that point on to 1800 CE. This parabola does not exactly fit the data wh ere the decrease in entropy occurs in association with all points beyond 200 CE, however, that is nothing more than the difference between expected data and observed data.
.png)
Fig. 9. A parabolic fit to skeletonized entropy data from 700 BCE to 1800 CE. The X-axis represents time in centuries and extends from 1000 BCE to 1800 CE. The Y-axis is entropy. The parabola extends from 700 BCE to 1800 CE and is concave down
It is only a short
intellectual step from investigating the parabolic nature of the skeletonized entropy graph from 700 BCE to
1800 CE to questioning if there is not the possibility of another and
earlier parabolic fit to the data at hand?
In fact, there is! (see Fig. 10) Here, the parabola is concave up and extends from 2800 BCE to 1200 BCE. The second order
regression equation of best fit is:
Y = 1.1326 – .072X + .0034X2, R2 = .9607. (Eq. 3)
.png)
Fig. 10. A parabolic fit to skeletonized entropy data from 2800 BCE to 1200 BCE. The axes are as defined in Fig. 9. This fitted parabola extends from 2800 BCE to 1200 BCE and is concave up
In regard to this particular phase of human history, the period begins with a phase of decreasing entropy until approximately 2000 BCE or slightly before and then entropy increases until 1200 BCE. One should note that the right side of this parabola does not achieve the height of the beginning phase. This latter date coincides with the time of the Bronze Age Collapse.
These two parabolic trends of history, the earlier concave up and the latter concave down, are separated by a period of 500 years in which there is a linear decline in entropy, this time period being from 1200 BCE to 700 BCE. The graph of this trend can be seen in Fig. 11. This period of change from an entropy maximum of approximately .93 in value to an entropy low of .73 at 700 BCE acts as a bridge between the two parabolic periods. The linear regression of this data yields:
Y = 1.5087 – .0328X, R2 = .9483 (Eq. 3)
![]()
.png)
Fig. 11. A linear regression of skeletonized entropy data from 1200 BCE to 700 BCE. The axes as defined previously. This linear regression represents a straight-line descent of entropy decrease from 1200 BCE to 700 BCE
.png)
Fig. 12. A synthesis of the three previous graphs showing regressed skeletonized data from 2800 BCE to 1800 CE. Axes as previously defined. The time represented is from 2800 BCE to 1800 CE. This graph allows a clear understanding of the positions of both parabolas and the linear transition between them
Fig. 12 is a composite of the last three Figs, 9, 10, and 11 and represents a period of time from 2800 BCE through to 1800 CE and is presented here as an amalgam of human history which involves alternating changes from the periods of decreasing entropy to increasing entropy but does so using both linear and non-linear patterns. The last step in this amalgamation will be the inclusion of the present entropy status (see Fig. 13).
To this point no representation of entropy change has been given from 1800 CE to 2000 CE. This is because the magnitude of entropy increase dwarfs the details of the previous graphs. With the removal of the data point for 1900 CE, this is shown in Fig. 13 which will be discussed in detail in the next section.
![]()
![]()
.png)
Fig. 13. Skeletonized entropy data from 2800 BCE to 2000 CE. This graph with axes defined as previously, represents the history of skeletonized entropy change from 2800 BCE to 2000 CE. The alternating periods of entropy decrease followed by entropy increase are quite visible as are the alternating periods of non-linear and linear change as are the alternating phases on linearity, i.e. negative slope followed by positive slope, and of non-linearity, i.e. concave up followed by concave down
Fig. 13 will be discussed in detail later in the Discussion, but it should be noted here that the level of entropy that the world-system is operating with is historically high and requires enormous energy for its maintenance.
Discussion
The hyperbolic pattern of both total world-system growth and maximum urban area population growth, as identified by von Foerster et al. (1960) and later greatly refined by Korotayev et al. (2006) represents a pattern of rapid growth that occurs far more rapidly than exponential growth. This growth is particularly explosive at the end of the growth phase, a phase that Russian researchers have labeled ‘the blow-up phase of growth’. Korotayev has further suggested that because of its uniqueness, this type of growth should be known as hyperbolic growth (for a graph of this mode of growth see Fig. 1a). Further if the data for hyperbolic growth is log-transformed, the plot of the transformed data is not linear but is increasing in slope at an increasing rate, that is it has the shape of a concave up power function, while data generated by exponential growth is linear with a positive slope.
It is therefore unsurprising, but is confirming, that the overall pattern of entropy change associated with sets of T, Cmax, and γ is also over the same period of time, the last 5,000 years of human history, hyperbolic in form (see Fig. 1b). As the world-system grows, it requires more and more energy and in fact there is positive feedback between energy access and system growth but to a lim it; all systems have limits. Consequently, as the energy content of the world-system increases, associated entropy does as well and does so in a parallel hyperbolic pattern, a pattern that may be more generally identified as greater-than-exponential-growth (GTEG).
It can be shown that such patterns of growth can be produced by positive feedback between elements within the system (about a very simple toy model of such feedback see Harper 2019). Consequently, as overall system energy level rises, so does attendant entropy in toto. In summary then, the hyperbolic pattern, or more generally GTEG pattern, is understandable with respect to overall system energy access. It is worth noting here that to date, that is at the current growing edge of history, the most recent initiation of the blow-up phase is associated with an energy tipping point that is in turn associated with the advent of the Industrial Revolution beginning about 1750 CE; a preferred date that most researchers cling to (however, see Grinin and Korotayev 2015 and Wallerstein 2004 and others with respect to the ontogeny of the world-system to that point).
Now it is time to investigate some of the finer details of entropy change over essentially the same period of historical time. For this purpose a process of removal of outlier points in the entire set of points will be employed, that is a process of simplification akin to stripping away skin and muscle, etc. to reveal the basic skeleton of the pattern; this process is denoted as skeletonization. from this point on. The initial skeletonization step will be to remove a single point, the final point of the data set, the one representing system entropy for the year 2000 CE. In doing so, the graph in Fig. 2 is produced; one which is far less smooth than what the hyperbolic pattern of Fig. 1b would suggest. A jagged and oscillatory process is very clearly visible. However, on closer inspection this pattern reveals broader embedded trends.
In Fig. 3 these trends are revealed more clearly and represent the periods of increasing and decreasing entropy. These periods of entropy change per trend extend in time over anywhere from three to seven centuries. The inflection point of entropy change is represented at peaks and troughs everywhere coincident with century points with the exception of one point, an unrepresented point lying somewhere between 100 BCE and 200 CE. However, it should be noted that these century-coincident points are most probably a function of the coarseness of the scale of the plot and do not reflect temporal reality. Even so, these inflection points may qualify as tipping points, as they are associated with significant changes in slope, specifically from positive to negative for peaks and negative to positive for troughs. It would seem that human history is associated with alternating periods of decreasing and increasing entropy.
Over the last 5,000 years of human history, there is a definitive pattern of phase of decreasing and increasing entropy; unquestionably alternating, but the periods of increasing entropy are on average shorter, 2.75 centuries as opposed to 4.75 centuries for the periods of entropy decrease. This difference in phase duration may be attributable to the processes of positive feedback being more pronounced during the periods of increase and as a result system limits were reached sooner. This is not unlike the current period of entropy change that is in the process of ending; it is very clearly a process of world-system entropy growth and one in which there is a positive feedback between population and technology. Here I would credit Boserup's reasoning (1993) that before ultimate world-system limits are reached, as world-system population continues to grow, within that increasing population will (always) be (some) minds intelligent enough and creative enough to solve society's (and civilization's) problems. However, intelligence and creativity per se are not enough to exceed ultimate energetic limits without first undergoing significant reorganization and reorientation, that is without the world-system model on which intelligence and creativity operate and refer to.
When comparisons between unskeletonized and skeletonized graphs are made, it becomes quite clear that there are any number of historical trends and events that produce the sets of removed outlier points. As shown in Fig. 3 during the first period of entropy decrease, the oscillations from 4200 BCE through to 1900 BCE are a result of the establishment of the first empire, the Akkadian Empire, and the (probable) combination of ecological overshoot in the face of diminished societal margin(s) of error all overlain by the climate change of that period. Other examples are easy to find. Specifically, the brief entropy increase of 1300 CE followed by the significant downturn to 1400 CE, a downturn that included climate change, famine, the Black Death, and significant politico-military turmoil (for the previous two examples of historical events exceeding the bounds of more broadly based historical trends see Figs 4, 5, and 6). There is one further outlier worth noting, an outlier trend actually, that of the period of entropy decrease from 200 CE to 700 CE, followed by the period of entropy increase from 700 CE to 1000 CE. This is noteworthy, because it represents a significant historical excursion from the basic pattern to be defined shortly.
If skeletonization of this already skeletonized data is taken one further step (see Fig. 6), it can be seen that the overall historical pattern can be reduced from four periods of entropy decrease alternating with entropy increase to three periods of alternating entropy decrease followed by entropy increase. This pattern is displayed in the bottom panel of Fig. 6. This reduced pattern is significant, because, whereas the pattern in the second panel of Fig. 6 shows four alternating periods of entropy decrease and increase, the three-period pattern has coincident with its peaks new and higher levels of maximum urban area magnitude. The fourth maximum, previously removed via graph skeletonization, does not have a maximum that coincides with a new and higher magnitude of Cmax, but rather returns the world-system of that time to the previous maximum of 1.2 million established at 200 CE. This is, of course, the historical excursion referred to previously, which will now receive further attention.
The period of time occupied by the Rome-Han Empires from about 300 BCE to approximately 200 CE, a time of empire zenith, was followed by a precipitous decline, a decline in entropy value, H, from approximately H = .91 to H = .75. This change in entropy was accompanied by a decrease in Cmax size from 1.2 million to 400,000, a decrease in Cmax size by 67 %. During this time the total world-system population either remained essentially static at 190 million people during three centuries from 200 CE to 500 CE or increased to 207 million by 700 CE, which, from the perspective of some, was a time clearly within the depths of the Dark Ages. (Note, however, that this is also a period of ecological restoration [Chew 2007]). This researcher can only surmise that the reduction in resources required by the salient empires of the time, Rome and Han certainly, but also (slightly) lesser empires such as the Kushan and Parthian Empires, brought about, due to ever increasing empire complexity (Tainter 1988; Bardi 2019), a total world-system downturn.
It is now at this point in the discussion appropriate to compare the patterns of entropy change over historical time with those of maximum urban area change, specifically as represented by lnCmax. Fig. 7 presents a two-panel graph in which the top panel is the previous skeletonized graph displayed in the bottom panel of Fig. 5 and also as an overlay in Fig. 6. It should be apparent upon inspection that the alternating period of decreasing and increasing entropy are coincident with the periods of stasis and of punctuation; specifically, the periods of stasis are coincident with the periods of decreasing entropy, and the periods of Cmax increase, that is punctuation, are coincident with the periods of increasing entropy. On applying the same process of skeletonization to the lnCmax graph as was applied to the original graph of entropy change over time (see Figs 2–6), rather than taking the natural logs of entropy values, one can see more clearly the previously mentioned temporal coincidence between discrete phases of entropy change and either stasis or punctuation with respect to Cmax size. How should these coincident phases of human history be explained?
While a detailed analysis is left for the future, a few words may now be offered in response to the previous question. Considering the periods of coincident entropy decline and stasis first and focusing initially on the period from 1400 CE to 1800 CE, a period of time in which Cmax magnitude stabilizes around a value of one million with only slight variation during these 400 years, significant entropy decline also occurs. H declines from around .90 to about .77, a decrease of some 14.4 %. What does this mean? Yes, the world-system became more urbanized and therefore more orderly. So how or in what way is this increased orderliness achieved? As a conjecture only, one can suggest that the system was becoming more efficient at accessing and using energy. A test of this conjecture would be, again in very general terms, to look for improved means of access, transport, and use of energy. (Be aware that increasing inequality may well be associated with this decrease in entropy.)
With regard to entropy increase and increasing Cmax population, I have even less to say. Unquestionably, the periods of increasing Cmax, and there are four, must accompany either increasing access to energy or the exploitation of new energy sources. The Industrial Revolution is a prime example of the latter, and ve-ry possibly the increasing urbanization from 700 BCE through to 200 CE and example of the former. However, both periods of increased Cmax urbanization involve significant coupling of previously extant but less well coupled processes; that coupling being a form of positive feedback, but in the form of hypercycle formation (Harper 2017d; Padget and Powers 2012; Eigen and Schuster 1977). Paradigm-shifting invention should also be included here as a formative process, not be confused with the process of hypercycle formation itself which is by default paradigm-shifting.
Even further skeletonization of the period of time from 700 CE to 1800 CE yields a parabola-like display of points, certainly with some gaps, for example the period of time from 200 CE to 1000 CE. This parabola-like display is shown in Fig. 9, which is also represented algebraically as a quadratic one (see Eq. [2]), an equation with an excellent fit to data of R2 = .9469. (Please note, as previously mentioned, that higher order polynomials fitted to the same data do have slightly better R2 values but the quadratic model will be used for its simplicity.) The quadratic model is not used to show causal relationships, but only to represent an underlying pattern, which can certainly serve as a standard of comparison.
An objection may be raised here about the reality of this pattern and the ephemerality of applying a quadratic equation to this particular display of skeletonized points. However, other similar models have been applied to data in a variety of other sciences. As an example of this, the Hardy-Weinberg Equilibrium (Hardy 1908; Weinberg 1908), and equilibrium that is fundamental to most if not all of population genetics, will be briefly discussed. This equilibrium, coincidentally represented by a quadratic equation, has necessary and sufficient conditions that when applied show that the equilibrium cannot exist! To name three of those conditions, an infinitely large population, a condition that cannot exist, an equal sex ratio, also an ephemeral condition, and the absence of disturbing factors such as mutation and selection, both of which have ubiquitous presence, whether one considers a representational genome or a population level gene pool. In light of these conditions not being applicable, then the implication is that the equilibrium itself cannot exist. So what then is the utility of the Hardy-Weinberg Equilibrium? Its utility is as a standard of comparison, the diversion from which motivates researchers to consider the action of real distorting factors.
One more comment in light of the previous: John Maynard Smith (1968) in his excellent little book Mathematical Ideas in Biology, suggested when discussing Target Theory, that a mismatch between observed and model-generated expected data has the potential to be far more revelatory than a match between expected and observed per se. If the expected does not materialize, then something fundamentally different may well be the cause; paradigmatic-shifting science de-pends on such events.
With the previous apologetics stated, it is now worthwhile to turn to the consideration of other parabolic and linear distributions apparent in the skeletonized data. As noted in the results, a second parabolic distribution, earlier in human history, appears from 2800 BCE to 1200 BCE. This parabolic distribution is shorter in duration than the previous one and is also concave up in position, being represented again by a quadratic equation with a slightly better coefficient of determination, R2 = .9607. It should also be noted that these parabolas are separated in time by a period of entropy decline that is linear and in which H declines from a maximum of .94 to a minimum of approximately .75 and having a fit of R2 = .9483. There is then an overall entropy pattern in which linear changes in system entropy are alternated with parabolic entropy changes and further that with respect to the linear changes, these alternate with negative and po-sitive slopes. Analogously, the parabolas themselves alternate between concave up and concave down positions. It should be noted, however, that with respect to the periods of increasing and decreasing entropy, these alternate throughout the history represented, that is from 2800 BCE to 2000 CE. It is the existence of two different modes of display that require attention.
Fig. 13 is a composite of Figs 9, 10, and 11 and suggests that the energetic exploitation of our species, at least since serious urbanization began, has resulted in coupled phases of increasing and decreasing entropy that may be represented as a combination of both parabolic and linear distributions. It makes a great deal of sense to label as increasing world-system order or decreasing world-system order decreasing and increasing periods of entropy respectively. Increasing urbanization as represented by increasing Cmax is equated with the maximum level of energy accessible at any time. Then accessing a greater level of energy is at least suggestive of increasing Cmax. However, as World-System population continues to grow, it appears that the periods of relative stasis, say, from 100 BCE to 1800 CE, would involve the spread of urbanization at levels lower than that of Cmax, (i.e., at urban area sizes less than Cmax).
The briefer phases of linear change, particularly, the linear change from 1200 BCE to 700 BCE, should be considered as a form of transition from an urban maximum at one level of energy access to a higher level of energy access, but at a lower level of Cmax. Thus, for example, the maximum urban area population at 1200 BCE was 160,000 people, while over the next 500 years, a period of time when world-system population grew to in one estimate, 162 million, from a base of 100 million, the Cmax magnitude declined to 100,000 people. What circumstances permitted world-system population to grow as it did is puzzling, but it can be speculated that climate changes and better crop production could be the basis for such a surge. Better and more complex trade networks could very easily contribute to conditions supporting this population increase. Given this, then the World-System response was to increase the magnitude of Cmax, which would automatically increase the frequency of lower levels of urbanization, in turn enabling the more efficient housing of the increased population. This pattern of population growth motivating increased urbanization from 700 BCE to 100 BCE, but interestingly at this time World-System population growth declined or remained the same after the initial surge of 700 BCE; it did not exceed 160 million until 100 CE.
A comment should be made here of the period of time from 200 CE to 1000 CE, which was previously recognized for its uniqueness with respect to alternating periods of decreased entropy and their relationship to Cmax magnitude. As also previously mentioned, the magnitude of Cmax dropped from 1.2 million to 400,000 and then returned to that level eight centuries later. Even so, over this same period of time the (average) Cmax remained around one million until 1800 CE, after which over two centuries it grew to a size of 35 million, that is approximately what it was as of 2000 CE. The significance of this period of time from 200 CE until 1800 CE was that the stasis value of one million for Cmax was maintained to the point that from 1400 CE onward there was relatively little fluctuation about this value, but if the conjectures made here prove true, energy access then did not change significantly during that period of time until the appearance of the Industrial Revolution.
In light of the periods of stasis occupying more time than the periods of punctuation, what historical trends should be looked for? Of course, one should expect urbanization at higher values, as well as more efficient use of the world-system resources. However, overshoot of maximum urban area magnitude (empirically) masks the embedded parabolic structure of the process and gives the impression of a shortened phase of entropy increase, which, of course, it is. However, when removal of outlier points occurs, the parabolic pattern clearly appears. It is this difference between observed and expected which should motivate further research with respect to why the overshoot of Cmax magnitudes occurs. In brief then, the empirical evidence for changes in entropy when compared with the theorized pattern of entropy change does not match. Of course, the question arises: Why?
Conclusions
1. The macroscopic view of both maximum urban area population and the entropy associated with the world-system supporting those maximum urban areas exhibit the same hyperbolic pattern of growth.
2. The fine scale of the entropy pattern over the last 5,000 years is revealed by a process of skeletonization in which outlier points are removed.
3. Initial skeletonization reveals an alternating pattern of periods, groups of centuries, of entropy decrease followed by entropy increase. The periods of entropy decrease are approximately 1.7 times longer than the periods of entropy increase.
4. At one level of skeletonization there are four periods of decreasing and increasing entropy. Further skeletonization reduces this number to three.
5. Further skeletonization again reveals two parabolic point distributions, which are separated by two shorter periods of linear change.
6. The parabolas by themselves are sequentially concave up followed by concave down, and the periods of linear change alternate between an initial period having a negative slope and a second period, the one we are currently in, having a positive slope.
7. A composite of these four entropy point distributions provides a model against which the types of world-system historical change may be compared.
8. The future of the world-system may in broad terms only be predicted, given the verity of the combined pattern of entropy change.
Acknowledgement
The author wishes to extend his heartfelt gratitude to Evgeniya Stolyarova for very professional editing of this paper.
[1] Personal communication.
[2] URL: http://www.census.gov/population/international/data/worldpop/table/history/php.
References
Bailey K. 1990. Social Entropy Theory. Albany, N.Y.: The State University of New York Press.
Bak P. 1996. How Nature Works: The New Science of Self-organized Criticality. New York: Pergamon Press.
Bak P., and Sneppen K. 1993. Punctuated Equilibrium and Criticality in a Simple Model of Evolution. Physical Review Letters 71(24): 4083–4086.
Bardi U. 2019. Before the Collapse: A Guide to the Other Side of Growth. New York: Springer.
Boserup E. 1993. The Conditions of Agricultural Growth: The Economics of Agricultural Change Under Population Pressure. London: Routledge.
Chandler T. 1987. Four Thousand Years of Urban Growth: An Historical Census. Harvard: Edwin Mellin Press.
Chew S. C. 2007. Recurring Dark Ages: Ecological Stress, Climate Changes, and System Transformation. New York: AltaMira Press.
Eigen M., and Schuster P. 1977. The Hypercycle: A Principle of Natural Self-Organization. Part A: Emergence of the Hypercycle. Die Naturwissenschaften 64: 541–565.
Eldredge N., and Gould S. J. 1972. Punctuated Equilibrium: An Alternative to Phyletic Gradualism. Models in Paleobiology / Ed. by T. J. M. Schopf, pp. 82–115. San Francisco: Freeman Cooper.
von Foerster H., Mora P. M., and Amiot L. W. 1960. Doomsday: Friday, November 13, A. D. 2026. Science 132: 1291–1295.
Grinin L., and Korotayev A. 2015. The Great Divergence and the Great Convergence. New York: Springer.
Hardy A. 1908. Mendelian Proportions in a Mixed Population. Science 28: 49–50.
Harper A. 2010. The Trajectory of the World System over the Last 5000 Years. History & Mathematics: Processes and Models of Global Dynamics / Ed. by L. Grinin, P. Herrmann, A. Korotayev, and A. Tausch, pp. 13–63. Volgograd: Uchitel Publishing House.
Harper A. 2017a. An Equation-Based Systems Approach to Modeling Punctuated Equilibria Apparent in the Macropattern of Urbanization over Time. History and Mathematics: Economy, Demography, Culture, and Cosmic Civilizations / Ed. by L. Grinin, and A. Korotayev, pp. 200–217. Volgograd: Uchitel.
Harper A. 2017b. The Punctuated Equilibrium Macropattern of World System Urbanization and the Factors that Give Rise to That Macropattern. Social Evolution and History: Studies in the Evolution of Human Societies 16(1): 86–127.
Harper A. 2019. A Toy Model Mechanism for Greater-Than-Exponential Human Population Growth. History & Mathematics: Big History Aspects / Ed. by L. Grinin, and A. Korotayev, pp. 43–51. Volgograd: Uchitel.
Korotayev A., Malkov A., and Khaltourina D. 2006. Introduction to Social Macrodynamics: Compact Macromodels of the World System Growth. Moscow: Editorial URSS.
Modelski G. 2003. World Cities: –3000 to 2000. Washington. D. C.: FA-ROS 2000.
Padgett J. F., and Powers W. W. 2012. The Emergence of Organizations and Markets. Princeton: Princeton University Press.
Shannon C. 1948. A Mathematical Theory of Communication. Bell System Technical Journal 27(3): 379–423.
Smith J. 1968. Mathematical Ideas in Biology. New York: Cambridge University Press.
Tainter J. 1988. The Collapse of Complex Societies. New York: Cambridge University Press.
Tiner J. 2006. The World of Physics. Green Forest, AR: Master Books.
U.S. Census Bureau. N. d. U.S. Census Bureau Historical Estimates of World Population. URL: http://www.census.gov/population/international/data/worldpop/table/history/php.
Wallerstein I. 2004. World-Systems Analysis: An Introduction. Durham: Duke University Press.
Weinberg W. 1908. Uber den Nachweis der Vererbung beim Menschen. Jahreshefte des Vereins für vaterländische Naturkunde in Württemberg. 64: 369–382.
Appendix
The following steps represent the procedure used to calculate the Shannon-Weiner entropy value as represented by the formula:
H = -Σpilnpi, this done for each set of T, Cmax, and γ. These are the data used to produce the entropy graphs over time, that is the last 5,000 years of human history, in this paper.
1. The foundation for the algorithm for calculating H is the frequency distribution, F = αC-γ, wh ere F is the frequency of an urban area population, C, and γ is a fitted constant. The remaining variable, α, is determined in the following way: If F = 1, then α = Cmaxγ.
2. If the urban area population size is Cmax for F = 1, then for F = 2,
C =
Cmax/21/γ, and for F = 4 = 22, C = Cmax/22/γ,
and by iteration, if F = 2m,
then C = Cmax/2m/γ.
3. Noting that the total urban area population for any given m is Tm = Cm 2m, and by substitution Tm = (Cmax/21/γ) 2m, or Tm = Cmax2m(1 - 1/γ). It should be noted that the ratio of Cm + 1/Cm = 2(1 - 1/γ).
4. Since the total population of the
world-system at any given time is the sequence: ΣCmax2m(1 - 1/γ). The total value of this
sequence is: T = Cmax[(1 – rm)/
(1 – r)], a formula taken from the mathematics of sequences and series,
wh ere
r = 2(1 - 1/γ).
5. In order to determine the entropy value for each set of T, Cmax, and γ, it is necessary to compute the magnitude of m for each such set using the formula: m = ln[T/Cmax(r – 1) + 1]/lnr.
6. The full range of m is then divided into equal fractions, in this case fourths, and the population for each fourth then determined. After this, the value of each population segment is normalized by dividing by the total population size for that level of m. This gives pi per fourth, and then H is easily determined by substitution and calculation of the summed product of pilnpi.
7. The details for determining the population
value for each fourth are as follows. Given the total population, Tm, one should determine the
population for 75 % of the total m
and subtract the latter from the former. The same should
be done for the next fourth by subtracting
the population value of 50 % from that of the value of 75 %. This
procedure should be repeated for the remaining two fourths of m and then it is
necessary to normalize each fourth by dividing by Tm.





