Вернуться на страницу ежегодника Следующая статья
Ранговое распределение
палеонтологических морских родов и протодемографические циклы* (Скачать pdf)
Алексей Александрович Фомин, Международный центр образования и социально-гуманитарных исследований
Обосновывается наличие в динамике рангового распределения палеонтологических морских родов по отрядам, классам и типам циклов, идущим в такт с циклами, которые получаются, если экстраполировать ранее обнаруженные демографические циклы с сокращающимися периодами от цикла к циклу в одно и то же количество раз в прошлое. Это не только указывает на прямую эволюционную преемственность между биологической и социально-экономической эволюциями (эволюционные циклы первой плавно перерастают в циклы последней), что имеет эволюционно-историческое и эволюционно-биологическое методологические значения, но и обладает практической ценностью: позволяет гораздо более точно прогнозировать будущую циклическую (с сокращающимися циклами) эволюцию человечества, а также уточнять значение точки сингулярности – момента, когда ускоренность человеческой эволюции формально обратится в бесконечность.
Ключевые слова: ранговое распределение, логоциклы, палеонтологические роды, гиперболический рост, точка сингулярности.
Введение. Постановка проблемы
В (Коротаев 2018) обосновывается наличие единой гиперболической закономерности роста интенсивности социально-биотических «революций» от возникновения жизни и до современности, причем примерно с той же точкой сингулярности, что и у гиперболического роста населения Земли. Это ставит фундаментальный, интригующий вопрос о причине такого единства социальной и биологической эволюции.
В (Фомин 2018в) было обосновано, что оно может быть связано с тем, что на некотором этапе биологической эволюции, когда ее темпы слишком возросли, новые биологические виды просто перестали успевать возникать достаточно интенсивно для того, чтобы стало возможным продолжение их гиперболического роста, поэтому рост продолжился в форме гиперболического роста видов человеческой деятельности и, как следствие, гиперболического роста числа людей. В связи с этим было показано, что в фанерозое (примерно после 541 млн л. н.) число морских видов, реконструированное по палеонтологическому числу родов, на единице площади их обитания подвержено тому же гиперболическому закону роста, что и народонаселение планеты. Маловероятно, что это случайность. А значит, и реальное число видов (и не только морских) росло, с точностью до константы, по тому же гиперболическому закону, что и народонаселение Земли.
Там же было рассмотрено и указание на возможность наличия протодемографических колебаний в динамике этого удельного числа видов – колебаний, которые совпадают по фазе с демографическими колебаниями, обнаруженными в (Фомин 2016), если последние экстраполировать в прошлое. Иначе говоря, картина может выглядеть так, что не только гиперболический рост числа морских видов плавно перерос в гиперболический рост населения, но и соответствующие, наложенные на гиперболический рост, колебания числа видов плавно переросли в демографические колебания. Что было бы одним из элементов разрешения отмеченной загадки единства гиперболического роста интенсивности социально-биологических «революций».
Упомянутые демографические колебания связаны со следующей фор-мулой, полученной в (Фомин 2016) для описания динамики народонаселения Земли (в млн человек) как функции времени t в годах:
|
232085,08/(2037 – t) + |
(1) |
Здесь первый член (в первой строке) – это гипербола, которая давно была хорошо известна (см., например: Капица 1992; 1996). Разве что у разных авторов оценка значения точки сингулярности (то есть когда народонаселение планеты формально обращается в бесконечность) может быть различным и не совпадать с 2037 г. Если для ее вычисления использовать только демографические данные и учитывать колебательную составляющую (второй член формулы (1)), то погрешность точки сингулярности вполне может составлять несколько десятков лет.
Второй член (1) (вторая строка) описывает колебательную составляющую в динамике народонаселения Земли. Это так называемые логоциклык[1]: цилы, продолжительность которых меняется (в данном случае – сокращается) со временем в одно и то же количество раз. Они широко распространены в динамике разных показателей финансовых рынков (Сорнетте 2003) и, судя по всему, имеют широкое эволюционное распространение не только в биологических системах: встречаются в динамике биоразнообразия, распространенности археологических культур (Фомин 2018а), в климате (Он же 2018б), в развитии землетрясений (см., например: Sor-nette, Sammis 1995), ледотрясений (см., например: Faillettaz et al. 2009) и оползней (см., например: Pralong et al. 2005), и поэтому имеют фундаментальное эволюционное значение. Данные циклы имеют точку сингулярности, когда их частота формально обращается в бесконечность (в (1) это значение совпадает с точкой сингулярности гиперболического роста и тоже равна 2037 г.).
Колебательные демографические спады, описываемые (1), соответствуют развитию кризисов в Мир-Системе, которые и вызывают замедление демографического роста. И, как отмечалось чуть выше, если эту формулу экстраполировать в прошлое, то колебательные подъемы/спады в ней могут как раз примерно совпадать с колебательными спадами в динамике плотности количества (морских) видов.
Но, как отмечалось в (Фомин 2018в), достоверно увидеть это не позволяет неполнота данных в динамике площади моря на территории нынешних континентов (которая была приближенно принята в качестве всей территории обитания морских палеонтологических находок для своего времени, благодаря чему и оказалось возможным вычислить динамику видовой плотности): по реконструкции этой величины у одних авторов протодемографические циклы в динамике плотности количества морских видов увидеть можно, у других – нет. В этой статье трудность прямой реконструкции протодемографических циклов преодолевается косвенной: благодаря обнаружению соответствующих циклов в динамике ранговых распределений[2] морских родов, которые идут синхронно с циклами (1), если последние экстраполировать в прошлое.
Показатель по линейным участкам рангового распределения
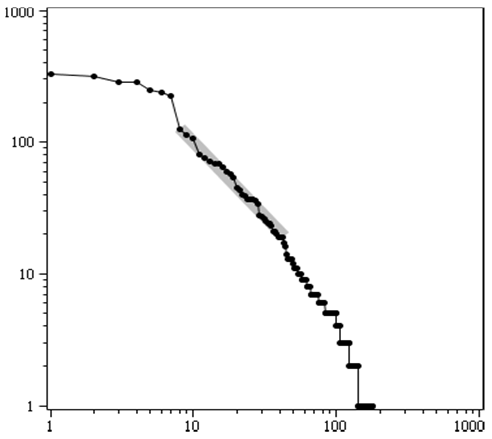
Рис. 1. Ранговое распределение по количеству палеонтологических морских родов по отрядам для промежутка времени 368,7―301,3 млн л. н. (соответствует третьей точке слева на рис. 3A) и его «линейная параметризация» (толстая прямая, получена минимизацией дисперсии: 1316,45/t1,12) для «линейного» участка. Ордината: число родов в отряде в десятичном логарифмическом масштабе, абсцисс: по-рядковые номера отрядов, расположенных в порядке убы-вания числа входящих в них родов. Данные: те же, что и на рис. 3
Ранговые распределения в какой-то степени позволяют избежать неполноты данных. Так как они обладают тем свойством, что если они линейны в двойном логарифмическом масштабе (как, например, на соответствующем участке рис. 1) и из них равномерно выкидывать точки (например, каждую вторую, каждую третью, каждые две вторых или каждые две третьих и т. д.), то показатель степени рангового распределения[3] от этого существенно не изменится, если производить его вычисление по всем точкам рангового распределения, кроме первой. Например, если имеется идеальное ранговое распределение некой величины с показателем степени, равным единице[4], состоящее из 1000 точек, то если из этого идеального рангового распределения выбросить все точки, кроме каждой сотой, то в результате получится распределение, показанное на рис. 1. Как видно, только самая первая точка стала существенно выпадать из линейной зависимости в двойном логарифмическом масштабе. Причем если до упомянутого прореживания точек показатель рангового распределения был по определению равен 1, то после он становится равным около 1,47, если его вычислять по всем точкам рис. 1, кроме первой. Иначе говоря, если ранговое распределение морских родов по тысяче отрядов имеет показатель степени, равный 1, и оно близко к идеальному (то есть отклонение от параметризующей гиперболы мало), и если неполнота данных отрядов составляет 99 % (то есть в палеонтологической летописи известен только 1 % от общего, реально существовавшего их числа), то вычисленный показатель рангового распределения по найденному 1 % отрядов будет равен 1,47, если вычисление производить по явно бросающемуся в глаза линейному участку. Можно показать, что если в описанном мысленном эксперименте оставлять каждую десятую точку исходного рангового распределения, то показатель степени получится равным 1,29. То есть неполнота данных уменьшилась в 10 раз, а показатель степени изменился всего примерно на 14 %.
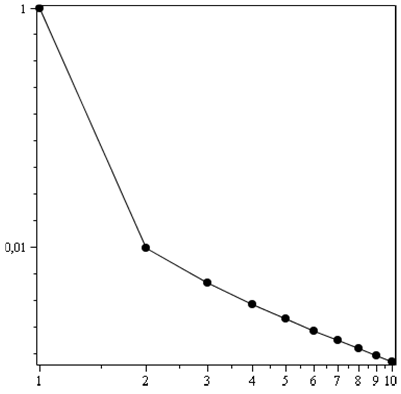
Рис. 2. Ранговое распределение, которое получается путем выкидывания из начального, идеального рангового распределения (с показателем степени, равным 1), состоящем из 1000 точек, каждой 99-й его точки
Иначе говоря, показатель рангового распределения должен очень слабо зависеть от неполноты палеонтологических данных, например, если рассматривать ранговое распределение морских палеонтологических родов по отрядам (как на рис. 1). Отклонение от линейности в двойном логарифмическом масштабе рангового распределения может быть связано не толь-ко с неполнотой данных, как это иллюстрирует мысленный эксперимент на рис. 2, но и с самой природой вещей: ранговым распределениям свойственно такое отклонение для ряда некоторых первых точек рангового распределения и для большего количества последних.
В динамике показателя ранговых распределений палеонтологических таксонов по отрядам можно увидеть циклы, соответствующие (протодемографическим) логоциклам. В силу вышесказанного алгоритм поиска показателя рангового распределения будет состоять просто в том, чтобы выделять в ранговом распределении линейный (в двойном логарифмическом масштабе) участок и по нему вычислять показатель.
Показатели ранговых распределений распространенности очень разнообразного набора объектов (в биологии, экономике, технике, в землетрясениях и т. д.) обычно имеют тенденцию быть близкими к единице. Это означает, что единица – значение устойчивости. И, соответственно, чем больше отклонение от нее, тем выше неустойчивость. Об этом значении как о значении стабильности часто говорит Б. И. Кудрин в своих работах, размещенных на сайте http://www.kudrinbi.ru (там же см. многочисленные примеры рангового распределения из разных областей).
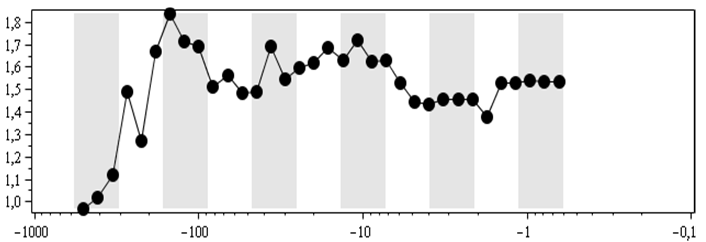
А. Вариант вычисления показателя степени рангового
распределения родов по отрядам для линейных (в двойном
логарифмическом масштабе) участков (как показано на рис. 1)
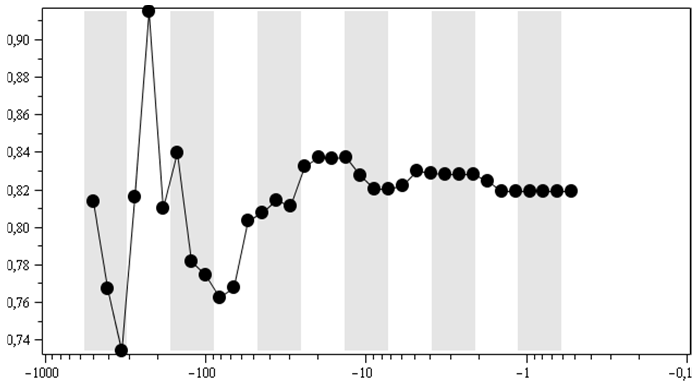
Б. То же, что и А, только показатель вычисляется
по всем точкам рангового распределения,
а не только по линейным участкам
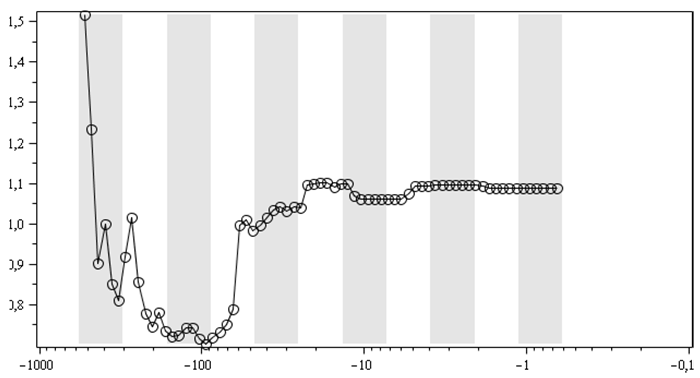
В. То же, что и Б, только для распределения
морских родов в классах
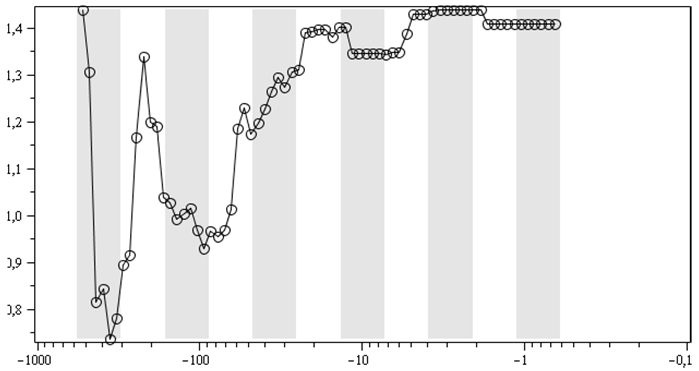
Г. То же, что и Б, только для распределения
морских родов в типах
Рис. 3.
Логоциклы в динамике показателя степени ранговых распределений для числа морских родов в отрядах (А, Б), классах (В), типах (Г)[5]. Абсцисс: календарные млн лет;
А, Б: точкам соответствует диапазон 501,57–0,52 млн л. н., В, Г – 526,86–0,66 млн л. н. Темные вертикальные полосы – вторые половины логоциклов, или, иначе, понижательные периоды колебательной компоненты из (1) – 2-й строки
Поэтому логично ожидать, что в периоды колебательных спадов реального количества биологических видов (то есть не палеонтологического, в котором может быть высока неполнота данных, уничтожающая нашу способность видеть реальные колебания) должно происходить особенно большое отклонение показателей ранговых распределения биоразнообразия от области стабильности (то есть от единицы). Чтобы проверить это напрямую, нужно реконструировать реальную колебательную динамику количества биологических видов. Что, как выше отмечалось, сейчас не представляется возможным. Но можно воспользоваться формулой для колебательной динамики народонаселения планеты. Ведь она (колебательная динамика народонаселения Земли) должна совпадать с колебательной динамикой количества биологических видов, если гиперболический рост последних с наложенными на него колебаниями действительно постепенно перерос в гиперболический рост населения Земли с наложенными на него колебаниями.
И это действительно имеет место, что иллюстрирует рис. 3A, на котором показана динамика показателя степени рангового распределения в варианте, когда она вычисляется по линейным (в двойном логарифмическом масштабе) участкам ранговых распределений. Причем «линейность», как правило, расположена в центральных областях ранговых распределений, как и показано на рис. 1.
Соответственно удаление показателя от значения стабильности означает увеличение нестабильности соответствующей системы (в рассматриваемом случае – биотической). Для вторых половин логоциклов характерны эволюционные кризисные явления. И рис. 3A действительно демонстрирует, что относительно крупные локальные колебательные отклонения показателя от единицы имеют тенденцию достигать своих максимальных значений именно во вторых половинах логоциклов (серые вертикальные полосы), а минимальные уровни (наиболее близкие к единице, наибольшая стабильность) – в первых половинах логоциклов (белые вертикальные полосы).
Но справедливости ради отмечу, что достаточно точное выделение «линейного» участка в ранговых распределениях, для того чтобы были видны колебания, соответствующие логоциклам, – совсем не тривиальная задача. И решить ее «на глаз» не получится. Поэтому для вычисления показателя рис. 3A была разработана и использована методика, суть которой состоит в том, что сначала область «линейности» выбирается на глаз, а потом немного сдвигаются ее границы – так, чтобы при параметризации минимизировать дисперсию, приходящуюся на одну точку. Причем эта минимизация осуществлялась, когда по осям графиков, аналогичных рис. 1, откладывались не соответствующие значения в логарифмическом масштабе, а логарифмы от значений, показанных на осях упомянутого рисунка. То есть зависимость превращалась в линейную без кавычек. Это было сделано для того, чтобы одинаковые отклонения от линейной зависимости для разных точек вносили одинаковый вклад в дисперсию. Как было установлено эмпирически, в противном случае метод поиска линейной области давал бы область, совсем не совпадающую с линейной областью, которая видится таковой визуально.
Показатель по всем точкам рангового распределения
В силу наличия момента субъективности в выборе линейной области у меня совсем нет стопроцентной уверенности в том, что результат пика биотической неустойчивости по показателю рангового распределения во вторых половинах логоциклов (2) на рис. 3A – это объективный результат. И для того чтобы хотя бы удостовериться в наличии логоциклов в ранговых распределениях на рис. 3Б, показана динамика показателя рангового распределения родов по отрядам, так же как и на рис. 3А, но без выделения линейной области. То есть в этом случае при вычислении показателя ранговых распределений оптимизация велась по всем имеющимся точкам соответствующих графиков ранговых распределений, аналогичных графику рис. 1. Как видим, на рис. 3Б отчетливо просматривается тенденция к достижению показателем пика в первых половинах логоциклов (белые вертикальные полосы) и падение или стабилизация показателя во вторых половинах логоциклов (серые вертикальные полосы).
Для ранговых распределений морских родов в классах и типах выбор линейного участка стал еще более проблематичным. Но и для них, для показателей ранговых распределений без такого выбора (то есть при вычислениях показателя степени рангового распределений по всем точкам соответствующих ранговых распределений), качественно получается схожая динамика, что отраженно на рис. 3В и 3Г. На них тоже отчетливо видно, что обычно всплеск идет в первых половинах логоциклов, а падение/стабилизация – во вторых. Для ранговых распределений палеонтологических морских отрядов по типам и классам линейных участков уже вовсе не существует.
Хотя для рис. 3Б, В, Г показатель, полученный не по «линейным» областям ранговых распределений, вообще говоря, уже некорректно интерпретировать с точки зрения стабильности/нестабильности по степени удаления от 1, но, по крайней мере, логоциклы в таком показателе, каков бы ни был его смысл, отчетливо видны.
Заключение
Наличие логоциклов в динамике показателя ранговых распределений палеонтологических данных может иметь далекоидущие последствия для уточнения точки сингулярности гиперболического роста населения Земли. Ведь в (1) это значение одновременно является критической точкой и для гиперболического роста, и для соответствующих логоциклов (когда частота их смены формально обращается в бесконечность). Таким же свойством могут обладать и логоколебания для разных показателей финансовых рынков: они описываются тем же выражением, что и (1), только с другими константами и с еще одной добавочной константой, приплюсованной ко всему выражению типа (1) (Сорнетте 2003). Только у них не обязательно будет происходить стремление показателя в особой точке к бесконечности, а может наблюдаться достижение им максимума с последующим обвалом (Там же). А, например, для индекса Доу-Джонса вместо логогиперболического роста (1) наблюдается квадратичный логогиперболический рост (Фомин 2018в: рис. 15), для инфляции фунта стерлингов – скорее, кубический логогиперболический рост (Там же: рис. 17). В обоих случаях основной тренд в точке сингулярности стремится к бесконечности. То есть основания для расчета точки сингулярности гиперболического роста населения Земли имеются не по гиперболическому тренду (первый член формулы (1)), а по колебательной составляющей. Но сделать это исключительно по данным народонаселения не представляется возможным с достаточной степенью точности для того, чтобы можно было однозначно определить точку сингулярности равной, скажем, не более 2060 г., поскольку задействован недостаточно большой промежуток времени. Точное знание этой точки сингулярности может быть чрезвычайно важным для прогнозирования эволюции Мир-Системы. Даже если логогиперболический рост населения Земли прекратится, то это еще автоматически не означает, что нелогогиперболическая эволюция не продолжится в другой форме: как, по сути, рассматривается в (Фомин 2018в), подобное в эволюции уже происходило, но не с количеством людей, а с количест-вом биологических видов, эволюция разнообразия которых сменилась эволюцией разнообразия человеческой деятельности (людьми). И развитие искусственного интеллекта пока дает все основания полагать, что автоматизированные системы (роботы) на какое-то время перед глобальной сингулярностью примут эстафету у людей. Поэтому более точное знание точки сингулярности может быть практически важным как для стратегического планирования государственной социально-экономической политики, так и для передовых IT-компаний, а вместе с ними и для большинства людей (если не сейчас, то в будущем).
И наличие, казалось бы, далеких от этого протодемографических логоциклов в динамике морского разнообразия позволяет значительно сузить погрешность нашего знания глобальной точки сингулярности. В даль-нейшем мы посвятим этому специальное исследование, а сейчас, забегая вперед, отметим, что учет циклов, подобных рассмотренным в этой статье (да и рассмотренные уже могут дать примерно такой же результат), позволяет вычислить глобальную точку сингулярности с точностью до плюс-минус пяти лет на уровне 2048 г.
Библиография
Капица С. П. 1992. Математическая модель роста населения мира. Математическое моделирование 4/6: 65–79.
Капица С. П. 1996. Феноменологическая теория роста населения Земли. Успехи физических наук 166(1): 63–80.
Коротаев А. В. 2018. Сингулярность XXI века в контексте Большой истории: математический анализ. Эволюция: Паттерны эволюции / Отв. ред. Л. Е. Гринин, А. В. Коротаев, с. 19–79. Волгоград: Учитель.
Марков А. В., Коротаев А. В. 2007. Динамика разнообразия фанерозойских морских животных соответствует модели гиперболического роста. Журнал общей биологии 68(1): 3–18.
Сорнетте Д. 2003. Как предсказывать крахи финансовых рынков. М.: Интернет-трейдинг.
Фомин А. А. 2016. О синтезе двух математических методов описания социально-экономической эволюции. История и Математика. Мегаисторические аспекты / Отв. ред. Л. Е. Гринин, А. В. Коротаев, с. 205–244. Волгоград: Учитель.
Фомин А. А. 2018а. Глобальная причина эволюционных кризисов, а также механизм выхода из них в случае социально-экономической эволюции. История и Математика: Социально-экономические аспекты истории и современности / Отв. ред. Л. Е. Гринин, А. В. Коротаев, с. 11–53. Волгоград: Учитель.
Фомин А. А. 2018б. Сквозная гиперболическая эволюция от биосферы до техносферы. Эволюция: Паттерны эволюции / Отв. ред. Л. Е. Гринин, А. В. Коротаев, с. 263–282. Волгоград: Учитель.
Фомин А. А. 2018в. Климат и человек: новый критерий связи и новый метод прогноза. XXIV Всемирный философский конгресс «Учиться быть человеком». Пекин, 13–20 августа 2018 г. Б. м.
Faillettaz J., Fumk M., Sornette D. 2009. Icequakes as Precursors of Ice Avalanches. URL: https://www.researchgate.net/publication/45859660_Icequakes_as_precursors_of_ice_avalanches.
Pralong A., Birrer C., Stahel W. A., Funk M. 2005. On the Predictability of Ice Avalanches. Nonlinear Processes in Geophysics 12: 849–861.
Sornette D., Sammis C. G. 1995. Complex Critical Exponents From Renormalization Group Theory of Earthquakes: Implications for Earthquake Predictions. Journal de Physique I 5: 607–619.
* Для цитирования: Фомин А. А. 2022. Ранговое распределение палеонтологических морских родов и протодемографические циклы. Эволюция: Эволюционная мозаика / Отв. ред. Л. Е. Гринин, А. В. Коротаев. Волгоград: Учитель. С. 90–101.
For citation: Fomin A. A. 2022. Rank Distribution of Paleontological Marine Genera and Protodemographic Cycles. Evolution: Evolutionary Mosaic / Ed. by L. E. Grinin, A. V. Korotayev. Volgograd: Uchitel. Pp. 90–101 (in Russian).
[1] Приставка «лого-» произошла из того, что в некотором логарифмическом масштабе времени эти циклы выглядят как постоянно-периодические. К примеру, см. ниже рис. 2.
[2] Ранговым распределением некоторого набора объектов, имеющих некое свойство «x», называется график зависимости величины x от ее порядкового номера, если пронумеровать объекты в порядке возрастания номера.
[3] Случай линейности рангового распределения для величины «x» в двойном логарифмическом масштабе означает ее степенную зависимость от ранга k: x~1/ka. Показатель степени «a» этой формулы и назван показателем рангового распределения.
[4] То есть эта величина, если серию ее значений расположить в порядке убывания, будет точно описываться формулой a/k, где k – порядковый номер, a – некая константа.
[5] Данные по динамике таксономической структуры, на основе которой вычислены показатели, были получены А. В. Марковым от любезно выславшего их ему Д. Д. Сепкоски, использовались в (Марков, Коротаев 2007); в них биоразнообразие было представлено как функция стратиграфических интервалов в геохронологической шкале 2005 г.





